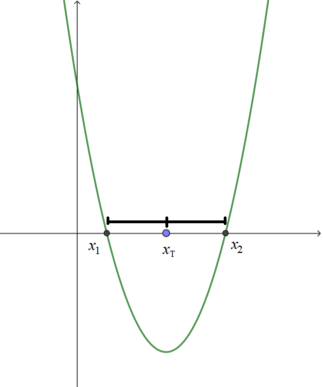
Ada metode lain untuk mencari akar persamaan kuadrat selain  rumus ABC yang biasa kita gunakan. Metode ini disebut dengan metode Po-Shen Loh. Untuk memahami bagaimana metode ini bekerja, tinjau gambar berikut:

Misal kita memiliki persamaan kuadrat $y=ax^2+bx+c$ yang memiliki akar-akar di $x_1$ dan $x_2$ seperti terlihat pada gambar.


Titik tengah antara $x_1$ dan $x_2$  kita namakan $x_{\text{T}}$ dimana:

  $$ x_{\text{T}} =\dfrac{ x_1 + x_2}{2}$$


Karena $ x_1 + x_2 = -\dfrac{b}{a}$, maka:

  $$ x_{\text{T}} = \dfrac{ x_1 + x_2}{2}= -\dfrac{b}{2a} $$


Perhatikan, jarak $x_1$ ke  $x_{\text{T}}$  sama dengan jarak  $x_1$ ke $x_{\text{T}}$. Kita namakan jarak ini $u$ sehingga:

  $$x_1 =  x_{\text{T}}-u$$

  $$x_2 =  x_{\text{T}}+u$$


Selanjutnya, karena   $x_1 . x_2 = \dfrac{c}{a}$, maka:

  $$\begin{align}
\dfrac{c}{a}&=( x_{\text{T}}-u )( x_{\text{T}}+u)\\
&= { x_{\text{T}}}^2 - u^2
\end{align}$$


 
Contoh: Tentukan akar-akar dari $y=x^2-2x+\dfrac{15}{16}$


Untuk soal ini kita ketahui: $a=1$, $b=-2$, $c= \dfrac{15}{16}$.


Metode Po-Shen Loh

Titik tengah  $x_T= - \dfrac{b}{2a} = 1$.

Sementara  $$x_1. x_2 = \dfrac{c}{a}= \dfrac{15}{16} $$ .


Maka

  $$\dfrac{15}{16} = 1 - u^2$$

  $$u^2 =\dfrac{1}{16} $$

  $$\rightarrow u= \dfrac{1}{4}$$ 


Kita peroleh

  $$x_1=x_T + u= 1 + \dfrac{1}{4} = \dfrac{5}{4}  $$

dan

   $$x_2=x_T-u = 1- \dfrac{1}{4} = \dfrac{3}{4}  $$



Rumus ABC

 $$\begin{align}
x_{1,2}&= -\dfrac{b}{2a}\,  \pm\, \dfrac{\sqrt {b^2-4ac}}{2a}\\
\\
&=1\,  \pm\, \dfrac{\sqrt {(-2)^2-4(1)\left(\dfrac{15}{16}\right)}}{2}\\ 
\\
&=1\,  \pm\, \dfrac{\sqrt {4-\dfrac{60}{16}}}{2}\\ 
\\
&=1\,  \pm\, \dfrac{\sqrt { \dfrac{64}{16} -\dfrac{60}{16}}}{2}\\ 
\\
&=1\,  \pm\, \dfrac{\sqrt {\dfrac{1}{4}}}{2}\\ 
\\
&=1\,  \pm\,  \dfrac{1}{4} \\ 
\end{align}$$ 


Kita peroleh

  $$x_1= 1 + \dfrac{1}{4} = \dfrac{5}{4}  $$ 

dan 

   $$x_2= 1- \dfrac{1}{4} = \dfrac{3}{4}  $$