Tinjau persamaan kuadrat:

 $$y=ax^2+bx+c \tag{1}\label{eq1} $$

Nilai yang memenuhi  $ax^2+bx+c=0$ disebut sebagai akar-akar dari persamaan kuadrat tersebut. Nilai ini dinyatakan oleh (rumus ABC):

  $$x_{1,2}= -\dfrac{b}{2a}\,  \pm\, \dfrac{\sqrt { \bbox[yellow]{b^2-4ac}}}{2a}  \tag{2}\label{eq2} $$


Bagian yang kita highlight dengan warna kuning disebut dengan diskriminan dari persamaan kuadrat tersebut. Berikut sejumlah kondisi terkait nilai dari diskriminan sebuah persamaan kuadrat:


1. $b^2-4ac < 0$

Di sini kita mendapatkan kondisi akar negatif. Untuk kondisi ini, persamaan  \eqref{eq1} tidak lagi memiliki akar-akar yang merupakan real ($\mathbb{R}$) dimana akar negatif adalah bilangan kompleks.

Contoh: Tinjau persamaan kuadrat $y=x^2 +x +1$

Persamaan di atas memiliki $a = 1,\, b=1,\,$ dan $c=1$


  $$D= b^2-4ac=1-4(1)(1) = 1- 4 = -3$$

  $$\rightarrow \sqrt{-3} =  \sqrt{3}  \sqrt{-1} =  \sqrt{-3} i$$ 


  $\sqrt{-3} i$ adalah bilangan kompleks ($\mathbb{C}$) yang nilainya tidak tercakup dalam ruang real.


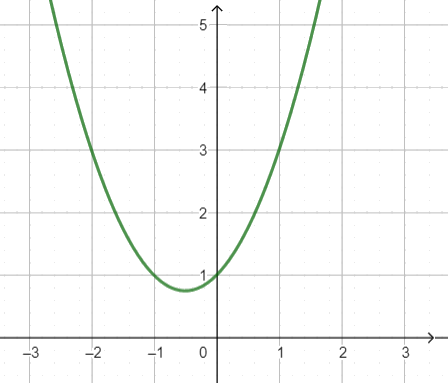
Untuk jelasnya, mari kita plot $y=x^2 +x +1$, hasilnya sebagai berikut:

Dari gambar di atas, kurva persamaan kuadrat yang kita tinjau tidak memotong sumbu $x$ atau dengan kata lain persamaan kuadrat tersebut tidak memiliki akar (real) atau dikatakan juga diskriminan dari persamaan kuadrat tersebut bernilai negatif. 


2. $b^2-4ac = 0$

Konsekuensinya  \eqref{eq2} menjadi


 $$x_{1,2}= -\dfrac{b}{2a}\,  \pm\, 0$$

 $$x_1 = x_2 =  -\dfrac{b}{2a} $$   


Dalam kondisi ini, persamaan kuadrat yang ditinjau memiliki akar tunggal atau dapat juga dikatakan kurva $y$ memotong (lebih tepatnya menyinggung) sumbu $x$ di titik $\left(-\dfrac{b}{2a}, 0 \right)$ .

Contoh: $y = x^2 +2x + 1$, maka $a=1, b= 2$, dan $c=1$


 $$b^2-4ac = 2^2 - 4 (1)(1) = 0$$

 $$ -\dfrac{b}{2a} = -\dfrac{2}{2} = -1$$


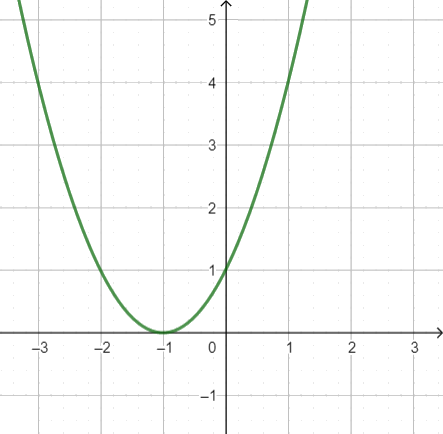
Kita peroleh akar dari   $x^2 +2 + 1$ adalah $x=-1$. Plot dari persamaan di atas diberikan oleh:

Sesuai dengan hasil perhitungan kita sebelumnya, kurva $y$ menyinggung sumbu $x$ di titik ($-1, 0$)


3. $b^2-4ac > 0$

Konsekuensinya, persamaan kuadrat  \eqref{eq1} memiliki dua akar real $\mathbb{R}$

 $$x_{1}= -\dfrac{b}{2a}\,  + \, \dfrac{\sqrt {b^2-4ac}}{2a}$$

 $$x_{2}= -\dfrac{b}{2a}\,  - \, \dfrac{\sqrt {b^2-4ac}}{2a}$$


Dalam kondisi ini, kurva persamaan kuadrat yang ditinjau memotong sumbu $x$ di dua titik yang disebutkan di atas.

Contoh: $y = x^2 -x - 2$, maka $a=1, b= -1$, dan $c=-2$


 $$D= b^2-4ac = (-1)^2 - 4 (1)(-2) = 9$$

Sekarang kita cari akar-akarnya sebagai berikut:

 $$\begin{align}
x_{1,2}&= -\dfrac{b}{2a}\,  \pm \, \dfrac{\sqrt {b^2-4ac}}{2a}\\
\\
&= -\dfrac{-1}{2}\,  \pm \, \dfrac{\sqrt {(-1)^2-4 (1)(-2) }}{2(1)}\\
\\
&= \dfrac{1}{2}\,  \pm \, \dfrac{3}{2}
\end{align}$$


Kita peroleh $x_1 = 2$ dan $x_2=-1$


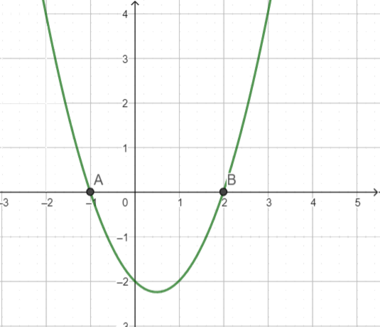
Plot persamaan $y = x^2 -x - 2$ diberikan oleh:


 

Perhatikan bahwa grafik tersebutk memotong sumbu-$x$ di $A(-1,0)$ dan $B(2,0)$. Hasil ini bersesuaian dengan yang kita dapatkan dari perhitungan sebelumnya.



~Kontributor: Dr. Muhammad Fakhrul Rozi Ashadi (schoolpad.id)


~Materi Terkait


~Problem Set Terkait: