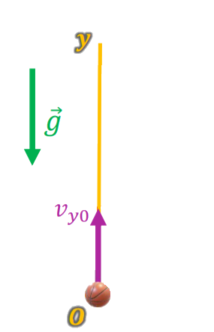
Budi melempar bola secara vertikal ke atas dengan kecepatan awal $v_0$.  Bola itu berada dalam pengaruh medan gravitasi sedemikian sehingga mendapatkan percepatan sebesar $g$ pada arah $y$ negatif sepanjang waktu seperti ditunjukkan pada gambar. Hambatan udara diabaikan.

Kecepatan awal dari objek tersebut dinyatakan sebagai $v_{0y}$

Diketahui ada pengaruh gaya eksternal yang memberikan percepatan pada bola tersebut pada arah $y$ negatif sebesar $g$.  Kecepatan bola tersebut pada arah $y$ dapat kita tuliskan:

  $$v_{y} (t) = v_{0y} - gt  \tag{1}\label{eq1} $$


Di sini benda mula-mula bergerak ke arah atas ($y$ positif) dan kecepatan $v_{0y}$ dan diperlambat sebesar $g$. Posisi bola tersebut sebagai fungsi dari waktu diberikan oleh:

  $$y(t)=\int v_y(t) dt =  \int  (v_0 \sin \theta_0 - gt)\, dt$$
   
  $$y=  v_{0y} t -\frac{1}{2} gt^2  + y_0 \tag{2}\label{eq2} $$

dengan $y_0=$ posisi awal benda (misalnya diambil $y_0=0$)



Pada saat  $v_y = 0$, ketinggian maksimum $H$ tercapai. Kita sebut waktu dimana ketinggian maksimum tercapai sebagai $t_H$. Dari persamaan \eqref{eq1} kita peroleh:


  $$\begin{align}
v_{0y} - gt_H &= 0\\
\\
v_{0y}  &= gt_H
\end{align}$$

  $$t_{H} = \frac{v_{0y}}{g}  \tag{3}\label{eq3} $$

Dari sini, bola yang semula bergerak ke arah atas ($y$ positif) selanjutnya akan bergerak ke arah $y$ negatif dan mencapai ketinggian awal dalam waktu $t_H$ pula (waktu naik = waktu turun). 

Perhatikan, kita dapat memperoleh hasil pada persamaan \eqref{eq3} dari  persamaan \eqref{eq2} melalui aplikasi turunan untuk mencari nilai maksimum/minimum [1].

Selanjutnya kita hitung ketinggian maksimum $H$ yang dapat dicapai sebagai berikut:

  $$\begin{align}
H &= v_{0y} t_H -\frac{1}{2} g\, {t_H}^2  + y_0\\
\\
&=  v_{0y}  \left(  \frac{v_{0y}}{g}\right) -\frac{1}{2} g \, \left(  \frac{v_{0y}}{g}\right)^2  + y_0\\
\\
&=  \left( \frac{{v_0}^2}{g} \right) - \frac{1}{2} g\, \left(\frac{{v_0}^2 }{g^{2}} \right) +y_0
\end{align}$$


  $$H =y_0  + \frac{{v_0}^2}{2g}  \tag{4}\label{eq4} $$


Kontributor:  Dr. Muhammad Rizqie Arbie (Fisika - ITB) 

Kurator:  Dr. Muhammad Fakhrul Rozi Ashadi (schoolpad.id)



Materi terkait

[1]   Aplikasi Turunan: Maksimum-Minimum



Problem set terkait