Tinjau limit dari fungsi $f$ di titik $x$ yang diberikan:

 $$\lim \limits_{h \to 0} \frac{f(x+h) - f(x)}{h} \tag{1}\label{eq1} $$
 
Apabila limit  \eqref{eq1} ada, maka nilai tersebut adalah nilai turunan fungsi $f$ di titik $x$.


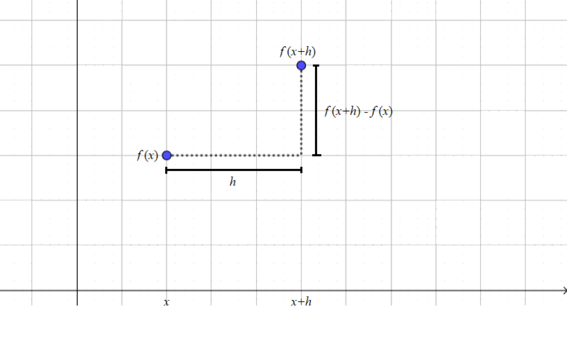
Sebagai ilustrasi, tinjau gambar berikut.

Mengikuti gambar di atas, persamaan \eqref{eq1} tidak lain adalah gradien garis yang menghubungkan titik $(x, f(x))$ dan $((x+h), f(x+h))$.  Dengan kata lain, nilai turunan sebuah fungsi di suatu titik merupakan gradien dari garis singgung fungsi tersebut di titik yang dimaksud.

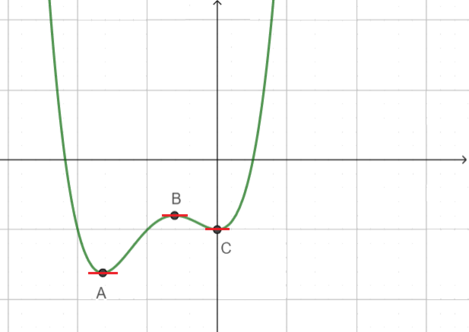
Tinjau suatu fungsi $f(x)$ yang plot nya ditunjukkan oleh gambar berikut:

Kita definisikan titik maksimum/minimum lokal sebagai titik dimana nilai $f(x)$ di titik itu lebih besar/kecil dari nilai disekitarnya. Kita menggunakan istilah lokal untuk menyatakan bahwa nilai yang dimaksud tidak harus yang paling besar/kecil untuk seluruh nilai fungsi. Berdasarkan definisi ini, titik $A$ dan $C$ adalah titik dimana fungsi $f(x)$ mencapai minimum lokal, dan titik $B$ adalah titik dimana $f$ mencapai nilai maksimum lokal. Secara umum titik $A, B$, dan $C$ disebut sebagai titik kritis dari fungsi $f(x)$

Titik $A, B$ dan $C$ memiliki kesamaan yaitu garis yang menyinggung $f$ pada titik-titik tersebut seluruhnya memiliki gradien $0$.

Berdasarkan tinjauan di atas dan definisi turunan yang diberikan pada persamaan  \eqref{eq1} kita dapatkan maksimum/minimum lokal dari sebuah fungsi terjadi di titik dimana turunan fungsi tersebut berinilai $0$.


Contoh 1. Tinjau fungsi $y = x^2 + 4x+ 1$

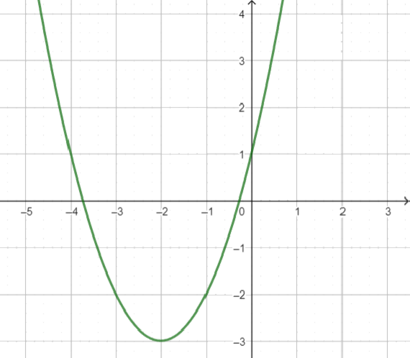
Plot dari fungsi tersebut diberikan pada gambar berikut:

Dari gambar di atas dapat kita lihat fungsi tersebut mencapai nilai minimum untuk $x=-2$ dimana $y(-2) = -3$.

Turunan dari $f(x)$ diberikan oleh:

  $$\dfrac {dy}{dx} = \frac{d}{dx} (x^2 + 4x + 1) = 2x + 4$$

  $$\dfrac {dy}{dx} = 0 \rightarrow 2x+ 4 = 0$$

  $$ x=-2$$

Hasil ini sesuai dengan yang diharapkan.



Kontributor:  Dr. Rizal Afgani (Matematika - ITB) 

Kurator:  Dr. Muhammad Fakhrul Rozi Ashadi (schoolpad.id)



Materi terkait




Problem set terkait